Regresión logística y algoritmo K-nn

En el afán del ser humano por reducir el esfuerzo para concretar una tarea se han desarrollado técnicas y conocimientos que suplen a la intuición. Una de estas tareas es la clasificación de objetos para tomar mejores decisiones. Con tal fin en la matemática, por medio de la estadística, se tienen métodos que permiten aproximar un modelo de clasificación de datos basados en una muestra. En este proyecto estudiamos dos de ellos: el modelo de regresión logística y el modelo de los $n$ vecinos más cercanos.
\section{Introducción}
La elección de la notación para los escritos científicos siempre es una tarea difícil, así que adoptaremos el mismo que los convencionalismos de la ESL. Usaremos $N$ para representar el número de datos distintos u observaciones en nuestras muestras y $p$ denotará el número de variables que están disponibles para hacer predicciones
Para poder clasificar los datos por medio de un algoritmo es necesario hacer suposiciones. Una de las suposiciones necesarias es pensar que existe algún modelo $f$ (aunque no lo conozcamos) que nos proporciona la clasificación de los datos
$$
Y = f(X) + \varepsilon,
$$
donde $X$ es el dato a clasificar, $Y$ la clase a la que pertenece y $\epsilon$ una variable aleatoria independiente de $X$ con media cero que se relaciona con el error introducido por el medio.
Con esta información tratamos de construir una estimación del modelo $f$ que llamamos $\hat{f}$ con la cual tratamos de aproximar $Y$. A esta aproximación la denotamos por $\hat{Y}$.
$$
\hat{Y} = \hat{f}(X)
$$
\subsection{Tipos de modelos}
Trabajaremos con dos tipos de modelos según la forma en que estos se construyen a partir de los supuestos.
\begin{itemize}
\item Modelos paramétricos Son aquellos que dependen de parámetros y estos parámetros se estiman bajo algún criterio del \textit{mejor ajuste} a partir de los datos muestra. Se espera que estos datos sean suficientemente buenos (y los parámetros bien escogidos) para que el modelo clasifique bien.
\item Modelos no paramétricos No dependen de parámetros sin embargo se ajusta el clasificador a partir de una muestra representativa de los datos a clasificar.
\end{itemize}
\section{Regresión Logística}
Supongamos que tenemos $N$ observaciones (con clases $Y=1$ o $Y=2$). En cierto momento nos encontramos un nuevo dato $X$ del cual no se conoce la clase que pertenece. Ahora nuestro trabajo es encontrar la función $p$ de probabilidad que nos indique la clase de $X$ en función de las $N$ observaciones previas. ¿Cómo podríamos modelar la relación ente $p(X) = P(Y=1|X)$ y $X$? Pues bien, sabemos que podemos utilizar un modelo de regresión lineal para representar dichas probabilidades:
\begin{equation*}
p(X) = \beta_0 + \beta_1X.
\end{equation*}
Sin embargo nos gustaría una función $P$ tal que modele la probabilidad (i.e. $\forall X$, $P(X)\in[0,\; 1]$). En la regresión logística, se usa la función logística,
\begin{equation}
\label{eqn:func_logistica}
P(X) = \frac{e^{\beta_0 + \beta_1^{T} X}}{1+e^{\beta_0 + \beta_1^{T}X}},
\end{equation}
donde:
\begin{itemize}
\item $\beta_0 \in \mathbb{R}$
\item $\beta_1^T$ es un vector con $p$ entradas.
\end{itemize}
Para ajustar el modelo (\ref{eqn:func_logistica}), usamos el método de la máxima verosimilitud. Esta técnica propone una función paramétrica para la clasificación binaria:
\begin{equation}
\label{eqn:func_L}
\mathcal{L}(\beta_{0}, \beta_{1}) = \prod_{i=1}^{N}p(X_i)^{Y_i}[1-p(X_{i})]^{1-Y_i}
\end{equation}
Los estimadores $\hat{\beta_0}$ y $\hat{\beta_1}$ se eligen de tal que manera que maximicen la función $\mathcal{L}$ (conocida como función de verosimilitud). Las máxima verosimilitud es una aproximación general que se usa para ajustar modelos lineales y no lineales
Si sustituimos la ecuación (\ref{eqn:func_logistica}) en (\ref{eqn:func_L}) y desarrollando obtenemos,
$$
\mathcal{L}(\beta_{0}, \beta_{1}) = \prod_{i=1}^{N} \left[ \frac{e^{\beta_0 + \beta_1^{T} X}}{1+e^{\beta_0 + \beta_1^{T}X}} \right]^{Y_i} \left[\frac{1}{1+e^{\beta_0 + \beta_1^{T}X}} \right]^{1-Y_i}.
$$
La función anterior es difícil de trabajar, puesto que está dado por un producto y es más difícil tratarla que si se tratara de una suma. Así, apliquemos el logaritmo para obtener:
$$
\ell(\beta_{0}, \beta_{1}) = \log\mathcal{L}(\beta_{0}, \beta_{1}) = \sum_{i=1}^{N}\left[ Y_i\left[ \frac{e^{\beta_0 + \beta_1^{T} X}}{1+e^{\beta_0 + \beta_1^{T}X}} \right] + (1-Y_i)\left[\frac{1}{1+e^{\beta_0 + \beta_1^{T}X}} \right] \right].
$$
Ahora, solo resta maximizar dicha función, a través métodos numéricos apropiados.
\section{Los $k$ Vecinos más Cercanos}
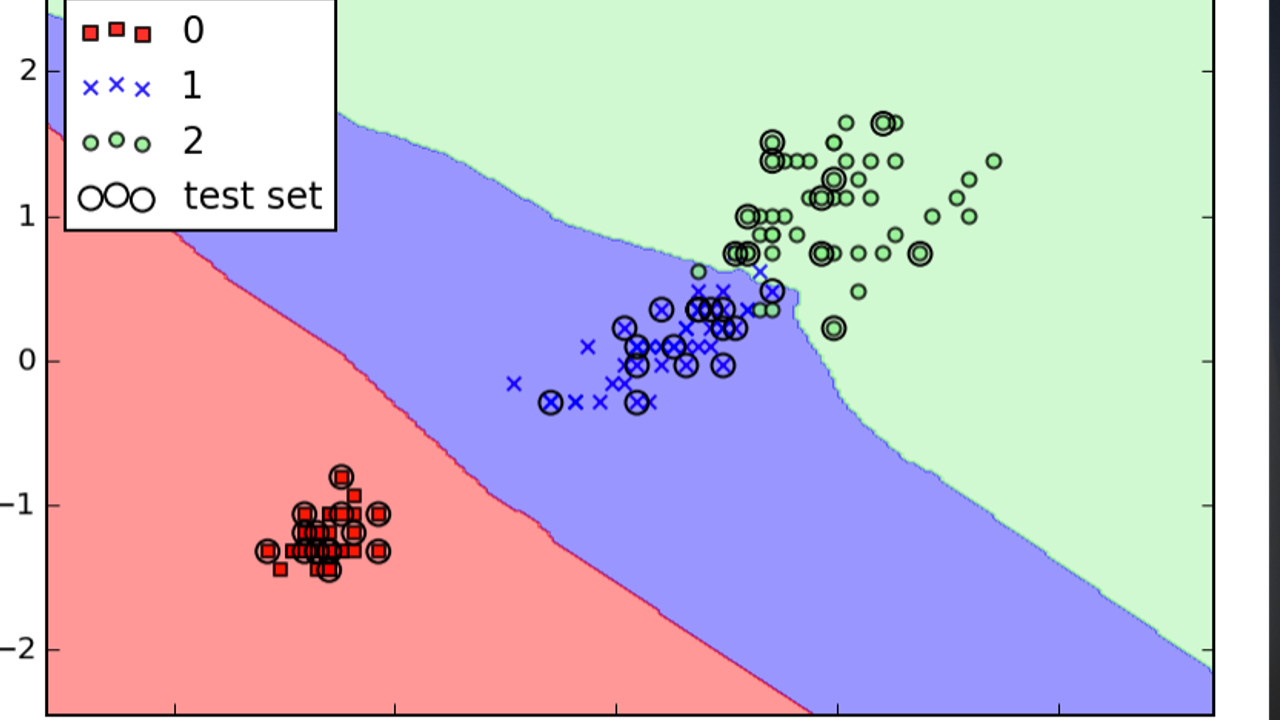
La idea básica sobre la que se fundamenta este clasificador es que una nueva muestra será clasificada a la clase más frecuente a la que pertenecen sus vecinos más cercanos ($k$-nn por sus siglas en inglés)
$k$-nn es un algoritmo perezoso, esto es, que durante el entrenamiento, solo guarda instancias y no construye ningún modelo, tampoco hace supuestos sobre la distribución que siguen los datos, por lo tanto es no paramétrico
Dado un conjunto de datos $ X= \left\lbrace X_1,\;X_2, \ldots ,\; X_p \right\rbrace $ y un conjunto de clases $ C= \left\lbrace C_1,\;C_2, \ldots ,\; C_m \right\rbrace $, el problema de clasificación es encontrar una función $ f:X \longrightarrow C $ tal que cada $ X_i $ es asignada a una clase $ C_j $
La fase de entrenamiento del algoritmo consiste en almacenar los vectores característicos y las etiquetas de las clases de los ejemplos de entrenamiento. En la fase de clasificación, la evaluación del ejemplo (del que no se conoce su clase) es representada por un vector en el espacio característico.
$ x = \left\lbrace x_1,x_2, … , x_m \right\rbrace $
Se calcula la distancia entre los vectores almacenados y el nuevo vector, generalmente se usa la distancia euclidiana
$$
d(x_i,x_j)=\sqrt{\sum_{r=1}^{p} (x_{ri}-x_{rj})^2}
$$
y se seleccionan los $ k $ ejemplos más cercanos.
El nuevo ejemplo es clasificado con la clase que más se repite en los vectores seleccionados. Este método supone que los vecinos más cercanos nos dan la mejor clasificación y esto se hace utilizando todos los atributos. Los valores de los atributos del i-esimo ejemplo con $ i \in \left\lbrace 1, \ldots , n \right\rbrace $ se representan por el vector p-dimensional
El problema de dicha suposición es que es posible que se tengan muchos atributos irrelevantes que dominen sobre la clasificación: dos atributos relevantes perderían peso entre otros veinte irrelevantes
Para corregir el posible sesgo se puede asignar un peso a las distancias de cada atributo, dándole así mayor importancia a los atributos más relevantes. Otra posibilidad consiste en tratar de determinar o ajustar los pesos con ejemplos conocidos de entrenamiento. Finalmente, antes de asignar pesos es recomendable identificar y eliminar los atributos que se consideran irrelevantes
La mejor elección de $ k $ depende fundamentalmente de los datos; generalmente, valores grandes de $ k $ reducen el efecto de ruido en la clasificación, pero crean límites entre clases parecidas. Un buen $ k $ puede ser seleccionado mediante una optimización de uso
La exactitud de este algoritmo puede ser severamente degradada por la presencia de ruido o características irrelevantes, o si las escalas de características no son consistentes con lo que uno considera importante.
 
\section{Conclusiones}
Pese a la formalidad con que se construye la teoría alrededor del clasificador de la regresión logística (o quizá debido a ella) este supone mayores dificultades al momento de la implementación para obtener mejores resultados. Por su parte el clasificador $k$-nn ofrece un principio sencillo y funcional para clasificar los datos
Sin duda la idea de optimizar para un conjunto de parámetros puede mejorarse por ejemplo encontrando cotas para estos mismos, quizá esto y algunas otras técnicas proporcionen un mejor acercamiento al resultado esperado
En esta sección se desarrollarán algunos experimentos en lo que pondremos a prueba los modelos poniendo a prueba la efectividad de éstos.