En la actualidad, las redes son inherentes en la vida cotidiana, ya que de alguna u otra manera las usamos sin siquiera notarlo. Por ejemplo: los teléfonos móviles, la computadoras, ciudades conectadas a través de carreteras. En general las redes, en su estructura general están formados por nodos conectados entre sí, donde la información fluye en uno o dos sentidos.
Un ejemplo de redes muy importante es el que forma el conjunto de neuronas en nuestro cerebro, en este caso, los nodos son las neuronas y las conexiones están dadas por el axón (parte de la neurona que envía la señal) y las dentritas (parte que recibe la señal). Durante la sinapsis de las neuronas reales ocurre entrada y salida de señales, y durante este proceso la señal se ve afectada, puesto que podría aumentar, disminuir o inhibirse la señal durante la comunicación. Luego, de alguna manera, se determina la activación de la neurona y finalmente esta ésta genera una salida.
Introducción
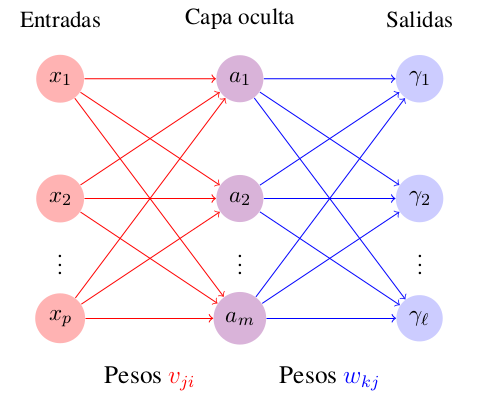
Las neuronas artificiales, basadas en las neuronas reales, se modelan a través de procesos matemáticos. Existen diversos modelos sobre neuronas artificiales con diferentes algoritmos que le dan solución a este problema. Los más usados consiste en tres capas, una de entrada conectada a una capa oculta que está conectada a una capa de salidas (ver Figura).
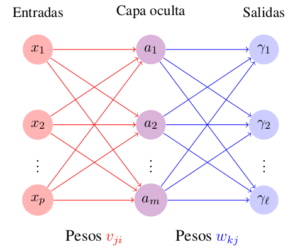
- Cada elemento en las entrada representa la información pura que se provee a la red.
- Los elementos de la capa oculta están determinados por cada entrada y los pesos sobre las conexiones entre la capa de entradas y la capa oculta.
- El comportamiento de cada salida depende de la actividad de las unidades ocultas y los pesos entre lo elementos de la capa oculta y cada una de las salidas.
Para dar solución a la red neuronal es preciso entrenar el modelo. Dicha solución está dada por un algoritmo de aprendizaje supervisado desarrollado en 1986 explica que podemos optimizar el error medio que se propaga durante la transmisión de la señal en la red.
Algoritmo de Propagación Hacia Atrás
El Algoritmo de Propagación Hacia Atrás se usa sobre un conjunto de entrenamiento
$$
\left\{
(\boldsymbol{x}_i,\; \bff{y}_i)\; |\; \bff{x}_i \in\mathbb{R}^p;\; \bff{y}_i\in \mathbb{R}^\ell;\; i=1,\; 2, \; \ldots, \; N
\right\}
$$
de $N$ señales de entrada con su respectiva salida. La función de activación $f$ se sugiere que sea la suma de las señales conocidas multiplicada por su respectivo peso, el cual indicará la perturbación que sufre la señal. Pongamos entonces
$$
f(\bff{x},\; \bff{w}) = \sum_{i=1}^p x_{i} w_{i} .
$$
Ahora se necesita elegir una función que genere una salida para cada neurona y una de las funciones más conocidas y útiles, en cuestiones de aprendizaje estadístico, es las función sigmoide (que es un caso particular de la función logística):
$$
g(x) = \frac{1}{1+e^{-x}}.
$$
Es una función continua sobre todos los números reales, con rango en el intervalo abierto $(0,\; 1)$. Se puede apreciar que crece asintóticamente uno. Por lo tanto, una excelente función que describa la salida de una señal es:
$$
g_k(\bff{x},\; \bff{w}) = g(f(\bff{x},\; \bff{w}_k)) =
\frac{1}{1+e^{-f(\bff{x},\; \bff{w}_k)}}.
$$
Entrenamiento de red neuronal con tres capas
A continuación se desarrollará el análisis para entrenar una red neuronal con tres capas, una capa de entrada, una capa oculta y una capa de salida (como se ilustra en la Figura \ref{fig:capas}). Nuestra tarea es hallar los valores de los vectores de parámetros $\bff{w}$ y $\bff{v}$ tal que el error cuadrático sea mínimo. En otras palabras, quisiéramos entrenar nuestro modelo de tal forma que obtengamos la salida deseada con el mínimo error. La expresión para el error para cada neurona en la capa de salida es:
$$
E_k = E(\bff{x},\; \bff{w},\; y_k) = \frac{1}{2} (\gamma_k – y_k)^2,
$$
donde $\gamma_k = g(f(\bff{a},\; \bff{w}_k))$ y $\bff{a}$ un vector con entradas $a_j = g(f(\bff{x},\; \bff{v}_j ))$. Es preciso notar que los índices toman valores $1 \leq i \leq p,\;\; 1 \leq j \leq m,\;\; 1 \leq k \leq \ell$. Finalmente, el error para red completa es la suma de los errores en cada neurona en la capa de salidas:
$$
E(\bff{x},\; \bff{v},\; \bff{w},\; \bff{y}) = \frac{1}{2} \sum_{k=1}^\ell(\gamma_k – y_k)^2.
$$
El error depende de las entradas, las salidas y los pesos. El algoritmo de la propagación hacia atrás, ajusta los pesos a través del método del gradiente descendiente.
Cada peso se actualiza usando el incremento
$$
\Delta w_{kj} = -\eta \parcial{E}{w_{kj}},
$$
donde el ajuste de cada peso $\Delta w_{kj}$ es el negativo de una constante $\eta$ multiplicado por la dependencia del peso anterior sobre el error de la red, i.e. la derivada de $E$ respecto a $w_{kj}$. Como el gradiente apunta hacia donde la función crece, se considera su negativo para minimizar el error y la constante $\eta$ indica la longitud del paso en cada iteración.
Regla de la Cadena
Utilizando la regla de la cadena, tenemos que:
$$
\parcial{E}{w_{kj}} = \parcial{E}{\gamma_k}\; \parcial{\gamma_k}{w_{kj}},
%
\hspace{1cm}
%
\parcial{\gamma_k}{w_{kj}} =
%\parcial{\gamma_k}{g}\;
\parcial{\gamma_k}{f}\;
%\parcial{a_j}{g_k}\;
%\parcial{g_k}{f}\;
\parcial{f}{w_{kj}},
$$
donde
\begin{eqnarray*}
\parcial{\gamma_k}{f}
&=& \frac{e^{-f}}{(1+e^{-f})^2}
= \frac{e^{-f}+1-1}{(1+e^{-f})^2} \nonumber \\
&=& \frac{1}{1+e^{-f}} – \frac{1}{(1+e^{-f})^2}
= \gamma_k – \gamma_k^2 \nonumber \\
&=& \gamma_k(1-\gamma_k)
\label{eqn:pp2}
\end{eqnarray*}
$$
\parcial{f}{w_{kj}} = a_{j},
\hspace{1cm}
\parcial{E}{\gamma_k} = \gamma_k – y_k.
$$
Por lo tanto
\begin{equation*}
\parcial{E}{w_{kj}} = a_{j} \gamma_k(\gamma_k – y_k)(1-g_k).
\label{eqn:errorw}
\end{equation*}
Finalmente el ajuste de los pesos es:
\begin{equation*}
\Delta w_{kj} = -\eta a_{j} \gamma_k(\gamma_k – y_k)(1-\gamma_k).
\label{eqn:delta}
\end{equation*}
Capa Oculta
Análogamente se procede para los pesos $\bff{v}_j$, en este caso se tiene:
$$
\Delta v_{ji} = -\eta \parcial{E}{v_{ji}},
$$
donde
$$
\parcial{E}{v_{ji}} = \sum_{k=1}^\ell \parcial{E}{\gamma_k}\; \parcial{\gamma_k}{v_{ji}},
$$
esto es porque cada $\gamma_k$ depende $v_{ji}$. Luego
$$
\parcial{\gamma_k}{v_{ji}} =
%\parcial{\gamma_k}{g}\;
\parcial{\gamma_k}{f_j}\;
\parcial{f_j}{a_j}\;
%\parcial{a_j}{g_j}\;
\parcial{a_j}{f_i}\;
\parcial{f_i}{v_{ji}}
=
\gamma_k(1-\gamma_k)w_{kj}a_j(1 – a_j)x_i.
$$
Por lo tanto
$$
\Delta v_{ji} = -\eta a_j(1 – a_j)x_i \sum_{k=1}^\ell (\gamma_k – y_k) \gamma_k(1-\gamma_k)w_{kj}.
$$
Análogamente podemos hacer este análisis para otra capa, calculando el error en función de las entradas y los pesos de la capa de salida. Es preciso notar que cada capa podría tener una cantidad diferente de neuronas. En la práctica, no es conveniente considerar muchas capas, puesto que el tiempo durante el proceso de entrenamiento crece exponencialmente. Una ajustado los pesos de la red se espera hallar el error mínimo cuando el gradiente $\nabla E(\bff{v}, \bff{w})$ sea suficientemente cercano a cero.
Conclusiones
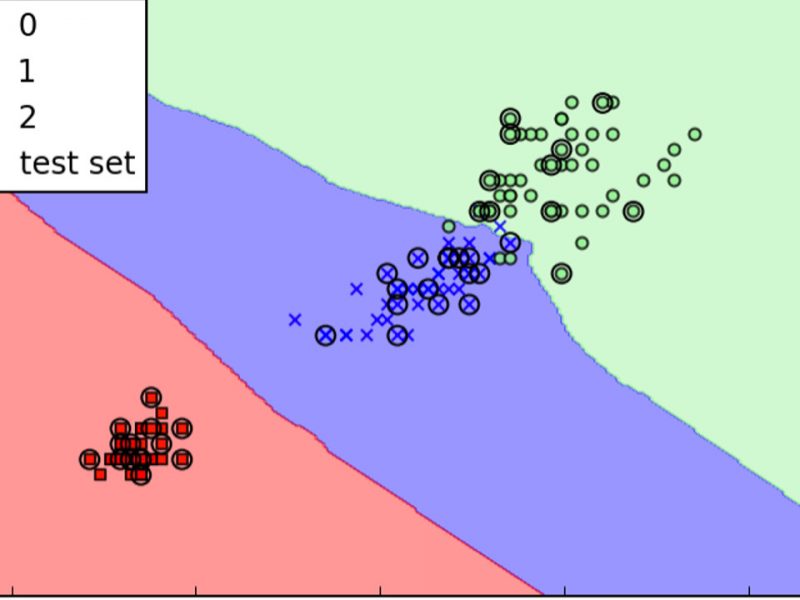
En conclusión, el entrenamiento de una red neuronal multicapa es relativamente sencillo y la implementación computacional no es tan complicada, ya que no es necesario hacer uso de librerías adicionales para del codificado del algoritmo. Además tiene muchas aplicaciones, se puede emplear una técnica para reconocimiento facial, análisis de patrones y como clasificador, entre otros. Por otro lado, como este método se basa en calcular derivadas, tiene una desventaja, la solución podría caer en mínimos locales por lo que será necesario aplicar el algoritmo varias veces con diferentes valores iniciales de los pesos.