Calcular la siguiente integra:
$$
\int_{0}^{+\infty}\dfrac{x^2}{x^6+1}.
$$
Solución.
Nos interesan los ceros del denominador, es decir, los $z\in \mathbb{C}$ tal que $z^6+1=0$. Estos números son
\begin{equation}
\label{eqn:r1}
c_k = \exp(i(\pi/6 + 2k\pi / 6) \hspace{10px} k=0, 1, \ldots, 5.
\end{equation}
De hecho para emplear la Proposición \ref{propo:semiplanoSuperio}, solo nos importan los puntos de la ecuación
(\ref{eqn:r1}) que están en el semiplano superior.
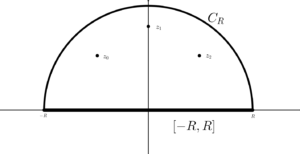
Sea $\Gamma_R = [-R, R]+C_R$ definida de la siguiente manera:
\begin{equation}
\label{eqn:gammaCurva}
\Gamma_R = \left\{
\begin{array}{ccc}
t &\mbox{si}& -R\leq t < R\\ R\exp(i\theta) &\mbox{si}& 0\leq \theta \leq \pi \end{array} \right. \end{equation} Notemos que para $z\in C_R$ se tiene $$ |f(z)| = \left| \dfrac{z^2}{z^6 +1 }\right| = \dfrac{|z|^2}{|x^6+1|}\leq \dfrac{|z|^2}{|z|^6-1} = \dfrac{R^2}{R^6-1}. $$ Así $$ \left| \int_{C_R}f(z)dz \right| \leq \int_{C_R}|f(z)| |dz|\leq \dfrac{R^2}{R^6-1}\pi R \longrightarrow 0 \hspace{10px} \mbox{cuando } R\rightarrow+\infty. $$ Hemos probado que $$ \lim_{R\rightarrow +\infty} \int_{C_R}f(z)dz = 0. $$ Ahora por la Proposición \ref{propo:semiplanoSuperio} $$ \int_{-\infty}^{+\infty}f(x) dx= 2\pi i \sum_{n = 0}^{2} \res{z=z_n} f(z)). $$ Ahora calculemos los residuos. Notemos que $p(z_k)=z_k^2\neq 0$, $q(z_k)=z_k^6+1=0$ y $p'(z_k) = 6z_k^5\neq 0$ con $k=0,\; 1,\; 2$. Lo anterior significa que los $z_k$’s son polos simples de $f(z)=p(z)/q(z)$. Así \begin{eqnarray*} \res{z=z_0} f(z) &=& \res{z=\exp(i\pi/6)}f(z) = \dfrac{p(\exp(i\pi/6))}{q'(\exp(i\pi/6))} \\ &=& \dfrac{\exp(i\pi/6)^2}{6\exp(i\pi/6)^5} = \dfrac{\exp(i2\pi/6)}{6\exp(i5\pi/6)}\\ &=& \dfrac{\exp(i\pi/3)}{6\exp(i5\pi/6)} = \frac{1}{6}\dfrac{\frac{1}{2}+i\frac{\sqrt{3}}{2}}{-\frac{\sqrt{3}}{2}+i\frac{1}{2}}\\ &=& \frac{1}{6} \dfrac{1+i\sqrt{3}}{-\sqrt{3}+i} = \frac{1}{6} \dfrac{1+i\sqrt{3}}{-\sqrt{3}+i}\cdot \dfrac{-\sqrt{3}-i}{-\sqrt{3}-i}\\ &=& \dfrac{-4i}{6\cdot 4} = \dfrac{-i}{6} \\ &=& \dfrac{i}{6i} \end{eqnarray*} \begin{eqnarray*} \res{z=i} f(z) = \dfrac{-1}{6i} =-\dfrac{1}{6i} \end{eqnarray*} \begin{eqnarray*} \res{z=\exp(i5\pi/6)} f(z) &=& \dfrac{\exp(i10\pi/6)}{6\exp(i25\pi/6)} = \dfrac{\exp(i5\pi/3)}{6\exp(i\pi/6)}\\ &=&\frac{1}{6} \cdot \dfrac{\exp(-i\pi/3)}{\exp(i\pi/6)} = \frac{1}{6} \cdot\dfrac{1-i\sqrt{3}}{\sqrt{3}+i}\\ &=& \frac{1}{6i} \end{eqnarray*}
Por lo que $$ \int_{-\infty}^{+\infty}f(x) dx = 2\pi i (\frac{1}{6i}-\frac{1}{6i}+\frac{1}{6i}) =\frac{\pi}{6}. $$ Como $f$ es par $$ \int_{0}^{+\infty}f(x) dx= \frac{1}{2}\int_{-\infty}^{+\infty}f(x) dx = \frac{\pi}{12}. $$
Proposición
Sea $f(z)=p(z)/q(z)$, donde $p$ y $q$ son polinomios. Suponga que los ceros de $q$ no están sobre el eje real y algunos de ellos están sobre el semiplano superior. Sea $\Gamma _R = [-R, R]+C_R$ donde $C_R$ es la curva dada por $z(t) = Re^{it}$ con $0\leq t \leq \pi$.
Si \begin{equation} \lim_{R\rightarrow +\infty}\int_{C_R}f(z)dz=0.
\label{eqn:intPropo} \end{equation} Entonces \begin{enumerate} \item Si $z_1.\ldots, z_n$ son ceros de $q$ en el semiplano superior \begin{equation} VP\int_{-\infty}^{\infty}f(x)dx = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z) \label{eqn:vpPropo1} \end{equation} \item Si $f(x)$ es par \begin{equation} \int_{-\infty}^{\infty}f(x)dx = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z) \label{eqn:vpPropo2} \end{equation} y \begin{equation} \int_{0}^{\infty}f(x)dx = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z) \label{eqn:vpPropo3} \end{equation} \end{enumerate} Establecer una Proposición análoga a la anterior. Sea $f(z)=p(z)/q(z)$, donde $p$ y $q$ son polinomios. Suponga que los ceros de $q$ no están sobre el eje real y algunos de ellos están sobre el semiplano inferior. Sea $\Gamma _R = [-R, R]+C_R$ donde $C_R$ es la curva dada por $z(t) = Re^{-it}$ con $0\leq t \leq \pi$. Si se cumple el análogo (\ref{eqn:intPropo}). Entonces \begin{enumerate} \item Si $z_1.\ldots, z_n$ son ceros de $q(z)$ en el semiplano inferior, entonces (\ref{eqn:vpPropo1}) \item Si $f(x)$ es par, se tiene (\ref{eqn:vpPropo2}) y (\ref{eqn:vpPropo3}). \end{enumerate} \begin{proof} Existe $R_0>0$ tal que $z_1$, $z_2$, $\ldots$, $z_n$ están en el interior de $\Gamma_{R_0}$. Por el Teorema de Cauchy del residuo para $R>R_0$
$$
\int_{\Gamma_{R}}f(z)dz = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z).
$$
A su vez
$$
\int_{\Gamma_{R}}f(z)dz = \int_{-R}^{R}f(x)dx+\int_{C_R}f(z)dz.
$$
Luego
$$
\int_{-R}^{R}f(x)dx = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z) – \int_{C_R}f(z)dz.
$$
Tomando el límite cuando $R\rightarrow +\infty$ tenemos
$$
VP \int_{-R}^{R}f(x)dx = \lim_{R\rightarrow \infty} \int_{-R}^{R}f(x)dx = 2\pi i \sum_{k=1}^{n}\res{z=z_k}f(z) – \lim_{R\rightarrow \infty} \int_{C_R}f(z)dz.
$$
Por (\ref{eqn:intPropo}) tenemos que se satisface (\ref{eqn:vpPropo1}).
\end{proof}
Calcular $\displaystyle \int_{-\infty}^{\infty}\dfrac{\cos 3x}{(x^2+1)^2}dx$.
Consideremos $\displaystyle h(z)=f(x)e^{iaz}$ con $f(z) = \dfrac{1}{(z^2+1)^2}$ y $a=3$. Notemos que $h(z)$ es analítica, salvo en $z=\pm i$.\\
Si $R>1$ y $\Gamma_R$ definida como en (\ref{eqn:gammaCurva}). De este modo
$$
\int_{\Gamma_R}h(z)dz = 2\pi i \res{z=i}h(z),
$$
es decir,
$$
\int_{-R}^R h(z)dz+\int_{C_R} h(z)dz = 2\pi i \res{z=i}h(z),
$$
esto implica que
\begin{equation}
\label{eqn:hzRes}
\int_{-R}^R h(z)dz = 2\pi i \res{z=i}h(z)-\int_{C_R} h(z)dz
\end{equation}
Notemos que para $z\in C_R$
$$
|f(z)| = \left|\dfrac{1}{(z^2+1)^2}\right|\leq \dfrac{1}{(|z|^2-1)^2} = \dfrac{1}{(R^2-1)^2} \longrightarrow 0 \mbox{ cuando } R\rightarrow \infty.
$$
Por el Lemma de Jordan
$$
\lim_{R\rightarrow \infty}\int_{C_R}f(z)dz=0.
$$
De (\ref{eqn:hzRes}) tenemos que
$$
\lim_{R\rightarrow \infty}\int_{-R}^R\dfrac{e^{3ix}}{(x^2+1)^2}dx=2\pi i \res{z=i} \dfrac{e^{3iz}}{(z^2+1)^2}
$$
Por otro lado, consideremos la función
$$
\phi (z) = \dfrac{e^{i3z}}{(z+i)^2}
$$
analítica en $i$ y $\phi(i)\neq 0$, entonces
$$
f(z) = \dfrac{\phi(z)}{(z-i)^2}
$$
tiene un polo de orden 2. Consideremos los siguiente
$$
\phi'(z)= \dfrac{3i(z+i)e^{3iz}-2e^{3iz}}{(z+i)^3}.
$$
Evaluando tenemos en $z= i$, tenemos
$$
\phi'(i) = \dfrac{3i(i+i)e^{3i^2}-2e^{3i^2}}{(i+i)^3} =
\dfrac{-6e^{-3}-2e^{-3}}{-8i} = \dfrac{-8e^{-3}}{-8i} = \dfrac{1}{ie^3}
$$
Por lo que
$$
2\pi i \res{z=i} f(z) = \dfrac{2\pi i}{ie^3} =\dfrac{2\pi }{e^3}.
$$
Así
$$
\lim_{R\rightarrow \infty}\int_{-R}^R\dfrac{\cos 3x}{(x^2+1)^2}dx+i\int_{-R}^R\dfrac{\sin 3x}{(x^2+1)^2}dx = \dfrac{2\pi }{e^3}.
$$
Por lo tanto
$$
\int_{-\infty}^{\infty}\dfrac{\cos 3x}{(x^2+1)^2}dx = \dfrac{2\pi }{e}
\hspace{10px}\mbox{ y }\hspace{10px}
\int_{-\infty}^{\infty}\dfrac{\sin 3x}{(x^2+1)^2}dx = 0.
$$
Demostrar que
$$
\int\limits_{0}^{\infty} \dfrac{\ln{x}}{(x^2+4)^2}dx = \frac{\pi}{32}(\ln{2}-1).
$$
$$
f(z) = \dfrac{\log{z}}{(z^2+4)^2}.
$$
Por el Teorema de Cauchy del Residuo tenemos
\begin{eqnarray*}
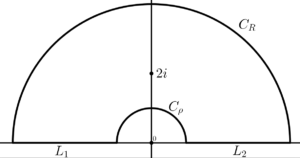
\int\limits_{\Gamma_{R ,\rho}}f(z)dz
&=&
\int\limits_{L_1}f(z)dz + \int\limits_{C_\rho}f(z)dz +\int\limits_{L_2}f(z)dz +\int\limits_{C_R}f(z)dz\\
&=&
2\pi i\res{z=2i}f(z).
\end{eqnarray*}
Lo anterior implica que
\begin{eqnarray}
\int\limits_{L_1}f(z)dz + \int\limits_{L_2}f(z)dz =2\pi i\res{z=2i}f(z) -\int\limits_{C_\rho}f(z)dz -\int\limits_{C_R}f(z)dz.
\label{eqn:l1l2}
\end{eqnarray}
Si $z\in C_\rho$, entonces
\begin{eqnarray}
|\log z| = |\ln|z|+i\theta| &\leq & |\ln|z||+|i\theta| \nonumber \\
&=& |\ln \rho|+|\theta| \nonumber\\
|\log z| & \leq & -\ln\rho+\theta ,
\label{eqn:logz}
\end{eqnarray}
por otro lado, tenemos
$$
|(z^2+4)^2| = |z^2+4|^2\geq ||z|-4|^2 = (\rho-4)^2 ,
$$
es decir,
\begin{equation}
\dfrac{1}{|(z^2+4)^2|}\leq \dfrac{1}{(\rho-4)^2}.
\label{eqn:z24}
\end{equation}
Por (\ref{eqn:logz}) y (\ref{eqn:z24}) tenemos que
$$
|f(z)| \leq \dfrac{-\ln\rho+\theta}{(\rho-4)^2}
$$
\begin{eqnarray*}
\left| \int\limits_{C_\rho}f(z)dz \right| &\leq& \int\limits_{C_\rho}|f(z)||dz|
\leq
\int\limits_{0}^{\pi} \dfrac{-\ln\rho+\theta}{(\rho-4)^2}\left( \dfrac{\pi \rho}{2}\right) d\theta \leq \int\limits_{0}^{\pi} \dfrac{-\ln\rho+\theta}{(\rho-4)^2}\left( \pi \rho\right) d\theta \\
&=&
\dfrac{\pi \rho}{(\rho-4)^2}\int\limits_{0}^{\pi} (-\ln\rho+\theta) d\theta = \dfrac{\pi \rho}{(\rho-4)^2} = \dfrac{\pi \rho}{(\rho-4)^2} (-\theta\ln\rho +\theta^2/2) \left|_{0}^{\pi}\right.\\
&=&
\dfrac{\pi \rho}{(\rho-4)^2} (-\pi\ln\rho +\pi^2/2)
=\dfrac{-\pi^2\rho\ln\rho}{(\rho-4)^2}+\dfrac{\pi^3\rho}{2(\rho-4)^2}.
\end{eqnarray*}
Observemos que
$$
\lim_{\rho \to 0}\dfrac{\pi^3\rho}{2(\rho-4)^2} = 0.
$$
Por variable real (regla de L’Hopital) se tiene,
$$
\lim_{\rho \to 0}(\rho \ln\rho) = \lim_{\rho \to 0}\dfrac{\ln \rho}{\rho^{-1}} = 0.
$$
Si $z\in C_R$, entonces (por simetría)
$$
\left| \int\limits_{C_R}f(z)dz \right| \leq \dfrac{-\pi^2R\ln R}{(R-4)^2}+\dfrac{\pi^3R}{2(R-4)^2}.
$$
Por variable real se puede ver que
$$
\lim_{R \to \infty}\dfrac{\pi^3R}{2(R-4)^2} = \lim_{R \to \infty}\dfrac{\pi^3/R}{2(1-4/R)^2}=0,
$$
además
$$
\lim_{R \to \infty}\dfrac{-\pi^2R\ln R}{(R-4)^2} = \lim_{R \to \infty}\dfrac{-\pi^2(\ln R)/R}{(1-4/R)^2}=0.
$$
Calculemos el residuo
$$
\res{z = 2i} f(z)= \dfrac{\log(z)/(z+2i)^2}{(z-2i)^2}.
$$
Notemos que $\phi(z) = \log(z)/(z+2i)^2$ es analítica en $z=2i$ y $\phi(2i)\neq0$, entonces $z= 2i$ es un polo de orden 2 de $f(z)$. Así
$$
\res{z=2i}f(z) = \phi ‘(2i).
$$
como
$$
\phi ‘(z) = \dfrac{\frac{1}{z}(z+2i)-2\log(z)}{(z+2i)^3}.
$$
\begin{eqnarray*}
\phi ‘(2i) &=& \dfrac{\frac{1}{2i}(4i)-2\log(2i)}{(4i)^3}=
\dfrac{2-2\ln(2)+i\pi}{(4i)^3} \\
&=& \dfrac{2-2\ln(2)+i\pi}{-64i}\\
&=& \dfrac{1-\ln(2)}{-32i}-\dfrac{\pi}{64}
\end{eqnarray*}
Ahora evaluemos la siguiente integral
\begin{eqnarray*}
\int\limits_{L_1}f(z)dz+\int\limits_{L_2}f(z)dz &=&
\int_{-R}^{-\rho}\dfrac{\ln |t|+i\pi}{(t^2+4)^2}dt+ \int_{\rho}^{R}\dfrac{\ln t}{(t^2+4)^2}dt\\
&=& \int_{\rho}^{R}\dfrac{2\ln |t|+i\pi}{(t^2+4)^2}dt\\
&=& \int_{\rho}^{R}\dfrac{2\ln |t|}{(t^2+4)^2}+\int_{\rho}^{R}\dfrac{i\pi}{(t^2+4)^2}dt.
\end{eqnarray*}
Tomano el límite cuando $\rho\to 0$ y $R\to \infty$
\begin{eqnarray*}
\int_{0}^{\infty}\dfrac{2\ln |t|}{(t^2+4)^2}+\int_{0}^{\infty}\dfrac{i\pi}{(t^2+4)^2}dt &=& 2\pi
i \left[
\dfrac{1-\ln(2)}{-32i}-\dfrac{\pi}{64} \right]\\
&=&
2\pi
\left[
\dfrac{\ln(2)-1}{32i}-\dfrac{\pi i}{64}
\right].
\end{eqnarray*}
Por lo tanto
$$
\int_{0}^{\infty}\dfrac{2\ln |t|}{(t^2+4)^2} = 2\pi\frac{\ln(2)-1}{32i}
\Longrightarrow
\int_{0}^{\infty}\dfrac{\ln |t|}{(t^2+4)^2} = \pi\frac{\ln(2)-1}{32i}
$$
Calcular
$$
\int_{0}^{2\pi}\dfrac{d\theta}{1+a\sin \theta},
$$
con $-1<a<1$. Tomando \begin{eqnarray*} \dfrac{1}{1+a\sin \theta} = \dfrac{1}{1+a[\frac{1}{2i}(z-\frac{1}{z})]} = \dfrac{1}{1+\frac{a(z^2+1)}{2zi}} = \dfrac{2iz}{az^2+2iz-a}. \end{eqnarray*} Así \begin{eqnarray*} \int_{0}^{2\pi}\dfrac{d\theta}{1+a\sin \theta} &=& \int\limits_{|z|=1}\dfrac{2iz}{az^2+2iz-a}\cdot \dfrac{1}{iz}dz = \int\limits_{|z|=1}\dfrac{2}{az^2+2iz-a}dz \end{eqnarray*} Notemos que \begin{eqnarray*} az^2+2iz-a = 0 \Longrightarrow z &=& \dfrac{-2i \pm \sqrt{(2i)^2+4a^2}}{2a} = \dfrac{-2i \pm \sqrt{(2i)^2+4a^2}}{2a}\\ & =& \dfrac{-2i \pm \sqrt{-4+4a^2}}{2a} = \frac{1}{a}(-i\pm \sqrt{-1+a^2})\\ &=& \frac{i}{a}(-1\pm \sqrt{a^2-1}). \end{eqnarray*} Pongamos $\displaystyle z_1 = \frac{i}{a}(-1+ \sqrt{1-a^2})$ y $\displaystyle z_2 = \frac{i}{a}(-1- \sqrt{1-a^2})$. Notemos que $$ |z_2| >1.
$$
Por otro lado, como $|z_1z_2|=1$, entonces
$$|z_1|= 1/|z_2|<1.$$
Nuestro integrando es
$$
f(z) = \dfrac{2/a}{(z-z_1)(z-z_2)} = \dfrac{\dfrac{2/a}{(z-z_2)}}{z-z_1}
= \dfrac{\phi(z)}{z-z_1}.
$$
Con $\phi(z) = \dfrac{2/a}{(z-z_2)}$ analítica en $z_1$ y $\phi(z_1)\neq 0$. Entonces $z_1$ es un polo de orden 1 de $f(z)$. Así
\begin{eqnarray*}
\res{z=z_1}f(z) &=& \phi(z) = \dfrac{2a}{\frac{i}{a}(-1+ \sqrt{1-a^2}) – (\frac{i}{a}(-1- \sqrt{1-a^2}))} \\
&=& \dfrac{1}{\sqrt{1-a}}
\end{eqnarray*}
Aplicando el Teorema de Cauchy del Residuo
$$
\int_{0}^{2\pi}\dfrac{d\theta}{1+a\sin \theta} = 2\pi i \left( \dfrac{1}{i\sqrt{1-a^2}}\right) = \dfrac{1}{\sqrt{1-a^2}}.
$$